作为所谓技术青年,我向来认为自己爱好理科,但从高中开始,我的理科成绩就一直是烂得可以,很奇怪。不过大学毕业的那段时间里,我无意中领会到我的兴趣爱好的培养都跟一本从小看到大的科普书有关,该书的统一书号是13031-841,嗯,1978年的中国书上还都没有ISBN的。今天不讲这个书,以后有机会再讲。今天讲玩具。因为最近很偶然的发现自己从小就对很多数学玩具有很深的兴趣,这些玩具对我的成长和学习也起到过不少的作用。
二进制在我玩过的数学玩具中占有很重要的一席之地,今天先聊聊这个。二进制中经常遇到2^N或2^N-1这样的值,所以这里说的就是广义上跟二进制相关的东西,包括几何级数。
一、猜年龄(属相、数字、etc)
魔术师拿出一把卡片,上面写有乱七八糟的数字,请观众找出包含自己年龄数字的那些卡片,然后魔术师就可以猜出观众的年龄。
这个魔术的演化版本实是在数不胜数,各种各样的道具也是层出不穷。我自己的做过的就不下十种,所谓的魔法卡片、魔法书什么的,各式各样但都万变不离其综。
这个游戏的原理现在来看实在是不值得一提。上网搜了一下,发现不知道这个游戏原理的人原来还不在少数……所以还是简述一下原理:
给卡片编上号,比如四张卡片,编号4,3,2,1。然后把数字转换成二进制,对于数字13=1101B,就在二进制位为1(即编号4,3,1)的卡片上写出上这个数字13。这样如果有人抽出了4,3,1这三张卡片,你马上可以知道他想的数字是2^3+2^2+2^0=13。……好像讲得太技术了,估计明白的人本来就明白,不明白的看了也没明白,算了,就这样吧……
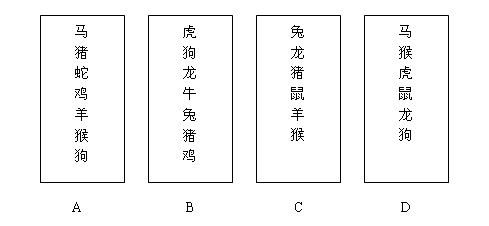
这个魔术原理太简单,所以还是要多用一些障眼法来实现比较好的效果,猜属相就是一个比较好的演化版本,这里就送大家一套猜属相的卡片吧:
ABCD四卡分别编号8421,找出哪几张就把对应编号相加,得出结果后减2,然后从依次排列的十二生肖中找到这个编号对应的动物即可。我的属相在ABD卡上出现,所以编号是8+4+1-2=11,所以属Dog。
有这些玩具的基础,若干年后看到两个所谓的面试智题力,就可以轻松的微微一笑,太简单了。
– 你让工人为你工作7天,给工人的回报是一根金条。金条平分成相连的7段,你必须在每天结束时给他们一段金条,如果只许你两次把金条弄断,你如何给你的工人付费?
– 现有1000个苹果,10个盒子,问各个盒子内应该分别放入多少个苹果,才能使得用户要买任意1至1000之间的一个苹果数,都可以给他(卖的时候是整个盒子卖,不能拆盒子的包装)。
二、九连环
其实九连环这个东西我一直没有玩过,只是从那经典的《十万个为什么》数学卷上了解到这个伟大的古老的中国玩具。
不过在我觉得“爸爸是万能的”的年纪,我让爸爸给我做过一些类似的玩具,其中一个宝塔环就是九连环有点相似,找不到完全一样的图片了,找到个类似的,爸爸做的比这个漂亮而且精致 :-)
在解宝塔环的时候,从上到下N个环中,如果要摆脱第N个环的束缚,就需要先把N个环套上,再解开所有N-1个。所以每解一层所需要状态变化都是上一层的2倍减1次。解开N个环需要经历的总的状态数是2^(N+1)-1。
而九连环里的二进制就更是复杂多了,九连环中的每个环都有上下两种状态,如果把这两种状态用0/1来表示的话,这个状态序列就会形成一种循环二进制编码(格雷码)的序列。所以解决九连环问题所需要的状态变化数就是格雷码111111111所对应的十进制数341。
九连环和宝塔环的状态序列的变化特征是每次状态变化都只会改变一个二进制位,在数字电路中这样的变化会比较平稳,而太多位的变化可能会带来很大的尖峰电流脉冲,所以用格雷码可以减少电路出错的可能性。
三、棋盘摆米和汉诺塔
印度古老传说中的国际象棋棋盘摆米的故事算不上是一个玩具,不过几何级数的神奇力量我也确实是实实在在的在数米粒的过程中体会到的。
要算是玩具的话,还是汉诺塔这个折磨过所有初学编程者的东东更好玩一些。小时候的我实在是没有那么强的动手能力去做三根细针和大小不一的圆盘,不过撕点大大小小的纸片,并在上面标注一下数字表示大小还是我可以做到的,于是这个玩具就被我这样粗制滥造出来了。
不知道是不是对二进制天生的敏感,相比上面那个宝塔连环,这个玩具似乎并没有为难到我,基本上这个玩具只陪伴了我不到一个小时的时间,我就发现,它跟棋盘摆米原来是一样的无聊……不过话说回来,刚开始的几分钟还是挺有意思的,所以还是拿这个简陋的玩具在朋友之间炫耀了一把。
高中的时候准备NOI竞赛的时候,汉诺塔做为学习递归的必修课倒是小小折磨了我一把,我那时对形参和实参实在是有点理解不了(我是BASIC出身,半路浅尝C,再半路学Pascal)。不过这段经历让我在大一C语言期末考试前颇是得意了一把,做为一道必考的题目,考试前一天我至少给不同的人讲了十遍汉诺塔的原理,我记得我那天嗓子有点哑……
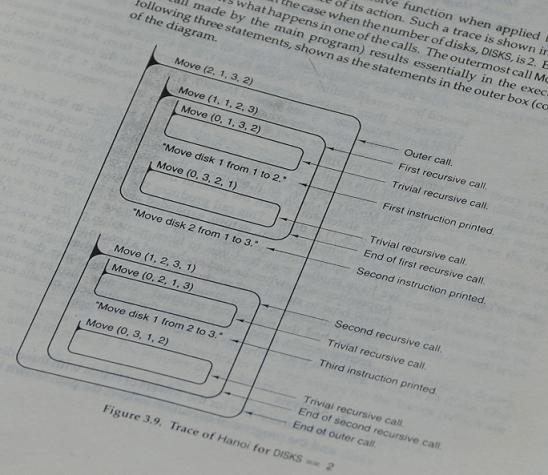
对于汉诺塔的递归程序,不知道有没有人尝试过去画它的(传统的)流程图,一定会失败的,传统的流程图完全没有办法去表达递归的思路。不过有一种图示可以比较好的画出递归的过程,这种流程图是我在我这辈子看的第一本英文技术书上看到的:Data Structure & Program Design in C,看这本书的是时候,我还正深受一些劣质中文Visual C++书之害,从此以后,看优秀的英文技术书就成为我坚定的信念。
与其跟学不会的递归纠缠不清,倒不如找找有没有非递归的汉诺塔解法。可惜虽然算法书上告诉大家:所有的尾递归都可以转化成迭代算法,结果却常常是搞成一个比递归还复杂的非递归实现。
《十万个为什么》第二套的数学卷2上讲过一种直观的非递归汉诺塔解法,很简单:
1. 把最小的圆盘向右移动到下一个位置,如果已经到最右边,就回到左边第一个位置
2. 把除最小圆盘所在位置的另外两个位置上的圆盘中较小的一个移动到大的上面(只可能有一种移法)
3. 重复1/2,直到所有盘子从一个柱子移到另一个柱子
不过不管怎么实现,完成神话中的64片金片的汉诺塔,需要步数总是二进制中64个1,正好相当于64位电脑的字长,对应的值就是2^64-1=18446744073709551615,如果一秒钟移一片,需要差不多5800亿年。